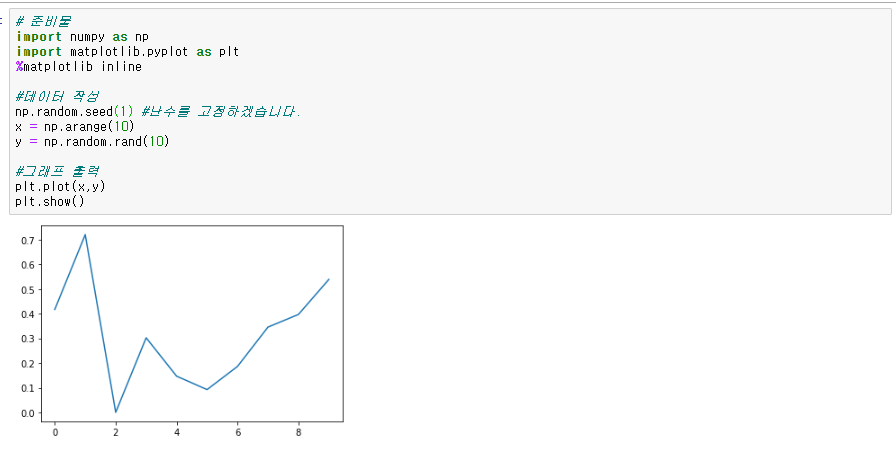
임의의 그래프를 그려보겠습니다.
그래프를 그리기 위해서는 matplotlib의 pyplot 라이브러리와 그래프 표시를 위하여 %matplotlib inline을 추가해줍니다.
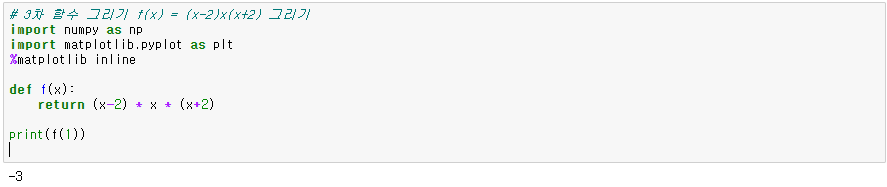
3차 함수 f(x)=(x-2)x(x+2) 그리기
f(x)=(x-2)x(x+2)의 그래프를 그려 봅시다. 이 함수의 수식이라면 x=-2,0,2에서 0이 되는 것을 쉽게 알 수 있지만, 그래프를 그려보지 않으면 잘 알수 없습니다.
먼저 함수 f(x)를 정의합니다.
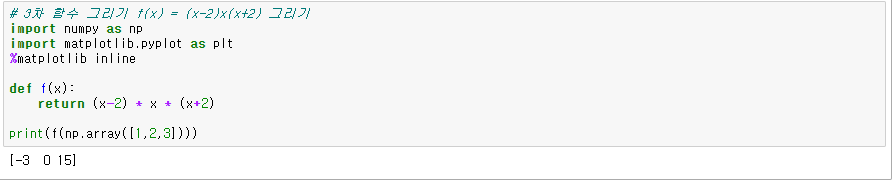
x는 ndarray 배열이며 각각에 대응한 f를 한꺼번에 ndarray로 돌려줍니다. 벡터의 사칙 연산은 각 요소마다 이루어지는 성질이 있기 때문입니다.
그래프를 그리는 x의 범위를 -3에서 3까지로 하고, 그 범위에서 계산한 x를 간격 0.5로 정의해 봅시다

np.arange(-3, 3, 0.5)로 하면 2.5까지의 범위를 다루므로, 3보다 큰 np.arange(-3, 3.5, 0.5)로 설정한 점에 주의하세요
그런데 그래프의 x를 정의하는 경우에는 arange보다 linspace라는 명령이 사용하기 쉬울지도 모릅니다.
linspace(n1, n2, n)하면 범위 n1에서 n2 사이를 일정 간격 n개의 구간으로 나누 값을 돌려줍니다

linspace를 사용하면 자연스럽게 n2가 x의 그래프에 포함되고, 그래프의 세밀함도 n으로 간단히 제어할 수 있습니다.
이제 그래프를 그려보겠습니다
그럼 여기서 x를 사용하여 f(x)의 그래프를 그려봅시다. 다음처럼 실행 결과가 나타납니다.
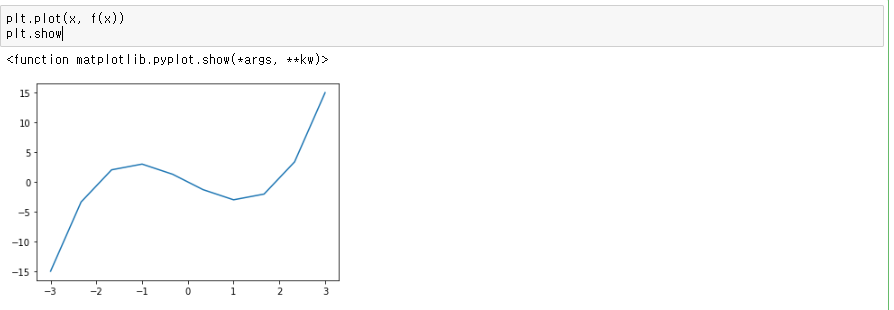
그런데 이 그래프는 정말로 x= -2, 0, 2일때 f(x)가 0의 값을 갖는지 여부를 알기 어렵습니다. 또한 함수의 계수가 변경될 때 그래프가 어떻게 변하는지도 궁금한 분도 있을 겁니다. 그래서 조금 손질한 그래프를 그려보겠습니다.
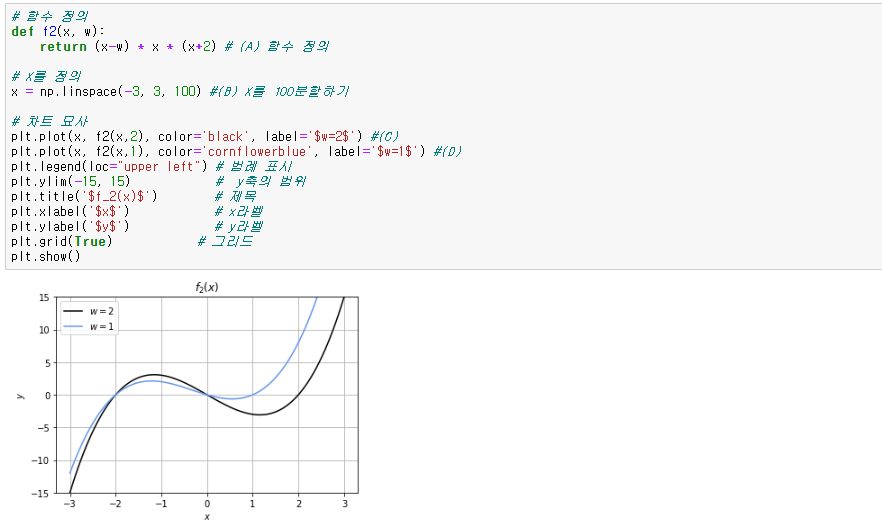
그래프도 매끄러워지고, 그리드와 라벨, 제목 범례가 들어갔습니다. 이제 함수 f(x)=(x-2)x(x+2)가 x축과 반나는 점은 -2, 0, 2라는 것이 명확해 졌습니다.(검은 선 : w=2). 또한 w=1일 때, 즉 f(x) = (x-2)x(x+2)이 되면 x축과 만나는 점이 -2, 0 ,1이 되는 것도 알 수 있습니다. (파란선 : w = 1)
그래프를 여러개 보여주기
여러 그래프를 나란히 표시하려면 plt.subplot(n1, n2, n)을 사용하여 전체를 세로 n1, 가로 n2ㄱ로 나눈 n번째에 그래프가 그려집니다. 번호는 왼쪽 위부터 1번째, 그 오른쪽이 2번째라는 식으로 할당됩니다. 맨 오른쪽까지 오면 한 행 내린 후 왼쪽 끝에서 시작합니다. plt.subplot의 n은 특별하게도 0이 아닌 1부터 시작하므로 주의해 주세요. 0을 지정하면 오류가 발생합니다.
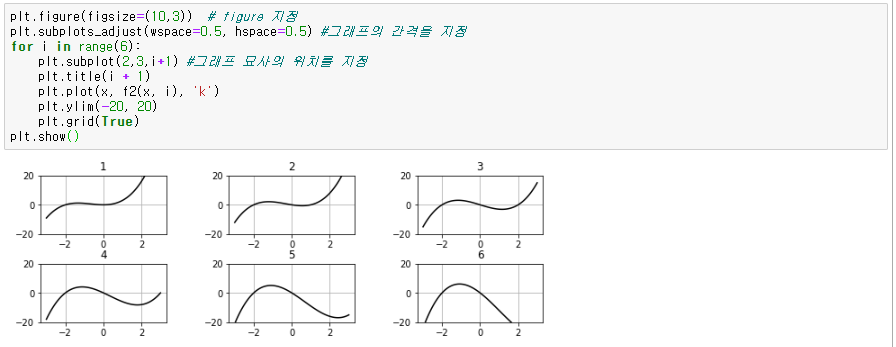
plt.figure(figsize=(w,h))는 전체 영역의 크기를 지정합니다.
가로 길이는 w이고 세로길이는 h입니다. subplot으로 늘어놓을 때, 좌우 및 상하 간격은 plt.subplots_adjust(wspace=w, hspace=h)로 조절할 수 있습니다.
'2020 > Machine Learning Deep Learning' 카테고리의 다른 글
| 케라스(Keras)와 텐서플로(TensorFlow) 설치 (0) | 2019.12.10 |
|---|---|
| Tensorflow 분류하기 (0) | 2019.12.09 |
| Tensorflow로 BMI측정 (0) | 2019.12.09 |
| Tensorflow basic (0) | 2019.12.06 |
| SKLearn 분류(IRIS) scikit-learn IRIS (0) | 2019.12.06 |



